熱血背包客莊ㄟ

Lecture 5- Evaluatiing arguments

by Marianne Talbot, university of Oxford 

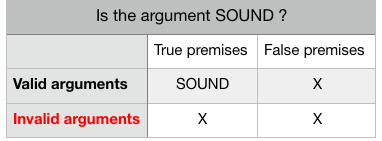
A good deductive argument is SOUND if and only if is :

1. Valid
2. Has true premises.

The truth of the premises is not a matter for logicians or those interested in critical thinking…

There are many ways in which we determine the truth or falsehood of premises. 

And these ways do not fall into the scope of a class on critical thinking…….

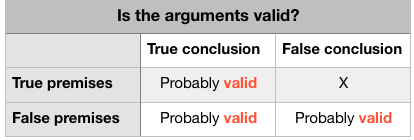
Validity is about true preserving.

Validity is very much of interest to logicians…

Because validity preserves truth…

If an argument is valid, then if its premises are true, 

We can certain its conclusion is true.

Validity is of interest to anyone who is concerning about truth…

Because we don’t know the truth of our premises 

And we often test the truth of premises by 

Constructing valid arguments and testing the truth of the conclusion 

EX1:

Hypothesis : smoking causes cancer

Prediction :  if smoking causes cancer, then every smoker will get cancer 

Test : each smoker get cancer… false 

EX2:

Hypothesis : all women are passive 

Prediction : Mrs. Thatcher is a woman 

Test : therefore Mrs. Thatcher is passive…false 

Both of 2 arguments exist at least one false premises, making the conclusion false.

So what is the relation of validity that everyone is so concerned with ?

Here is the best theory that philosophers and mathematicians can come up with ?

Claim about the validity

If and only if …

There is no possible situation in which..

All premises are true…

And its conclusion is false.

Beware:

It is the possibility of the combination…

…of true premises and false conclusion…

That is ruled out by an argument being valid 

this is the key!!!!

And it is the possibility of the combination 

Of true premises and false conclusion that is rule out by an argument being valid…

Not just the actuality of the combination of true premises and false conclusion…

So, faced with an argument whose validity we are trying to determine, we must ask…

1. ARE the premises true and conclusion false together in actuality ???
2. COULD the premises be true and the conclusion false together in some situation???

Could the argument be valid?

(A) the premises of the argument are false… YES

EX: if its Friday, Marianne is wearing jeans….false  

       It is Friday….false 

       Therefore, Marianne is wearing jeans…but it is an argument being valid

(B) the premises of the argument are true and the conclusion is true…YES

(C) the premise of the argument are true and the conclusion is false… NO

If the premises COULD be true…

TOGETHER WITH the conclusion being false…

Then….

The argument is invalid.

Otherwise it could be valid.

Valid or not ?

Premise: 2+2=5… contradiction, so there is no possibility of 

Conclusion: Grass is green.

Is there a situation in which the premises could be true and the conclusion false ?….

valid and must be valid, also by arithmetic principle

Because the definition—There is no possible situation in which..

{ All premises are true…

And its conclusion is false. } 

But how about…..

Grass is green.

2+2=4…arithmetic principle.

Is there a situation in which the premises could be true and the conclusion false ?

It is a valid argument, 

because there is no situation that the question mentioned. 

And it must be valid.

Because you can not prove “2+2=4” is false, which is a arithmetic principle.

2 of the example above are paradox entailment—although it’s not convincing, but still valid by satisfying the definition.

SO, you can put anything you like and any garbage you want into premises, but still the argument is  valid. 

Venn diagram to help judge validity: 

Premises actually true and conclusion actually true

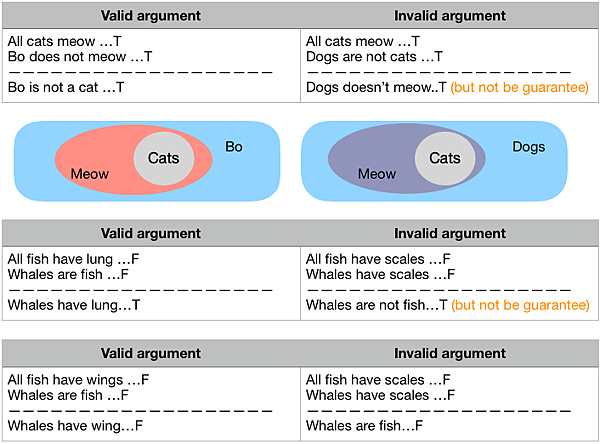
Counterexample to judge validity:

Set out logic book style 

If it’s snowing, the mail will be late 

It is snowing 

Therefore, the mail will be late 

If it’s snowing, the mail will be late 

the mail will be late 

Therefore, it is snowing 

If negate the conclusion 

If it’s snowing, the mail will be late 

It is snowing 

It is not the case that the mail will be late 

If it’s snowing, the mail will be late 

the mail will be late 

It is not the case that it is snowing 

We then consider whether the set of sentence 

consisting of the premises and 

The negation of the conclusion is consistent 

I.e. they could be all true together.

So, 

If the counterexample set is consistent then the original argument is invalid.

If the counterexample set is not consistent  then the original argument is valid

第五講內容滿多的，但是就服務一個原則就是，我們要找一個是非常健康非常適當的『演繹』argument時，必須有兩個條件，前提必須為真，然後argument必須有效，好拉這就是演繹法的論辯，當中還有提到valid這個字眼，這又要繼續細分下去囉，有效的情況表示，整個argument當中，『沒有』前提是真的並且結論是假的情況，這叫做『有效』，那這都是表面上的定義，實際上如何解決GRE那就要來看看筆記最後的一句話了，總的來說，假設題目問到weaken或是cast the doubt題型，正好好死不死，選項你看到有『反例』出現，這表示嘿嘿，答案就是他了。

以上來自牛津大學教授上課筆記希望能幫上忙，喜歡，或是不喜歡還是有錯誤，歡迎留言指教，謝謝!!